抱歉，您的浏览器无法访问本站
本页面需要浏览器支持（启用）JavaScript
了解详情 >

二叉树题目算法题目整理(附代码)

技术向C++算法
次浏览

字数：3.6k 字

时长：18 分钟

@auther by sizaif

说明：
由个人整理，部分题目是王道的题目,已经经常会考的点。
因个人代码风格,已经stack和queue的代码实现不同,代码略有不同之处，
但总体思想是正确的
有错误之处,欢迎指出
by sizaif

@TOC

二叉树

code 
++
/**
* 树结构
*/
typedef struct Node{
    char x;
    struct Node *lson,*rson;
}Tree,*BiTree;


typedef struct Queue{
    //自己构造队列
    BiTree *x;
    int front;
    int rear;
    void Initqueue()
    {
        front=rear=0;
        x =(BiTree *)malloc(MAX*sizeof(Tree));
    }
    void POP()
    {
        front=(front+1)%MAX;
    }
    int length()
    {
        return (rear-front +MAX)%MAX;
    }
    bool emptys()
    {
        if(front==rear)
            return 1;
        return 0;
    }
    void Push_back(BiTree T)
    {
        if((rear+1)%MAX==front)
            return;
        x[rear]=T;
        rear=(rear+1)%MAX;
    }
    BiTree Getfront()
    {
        if(front==rear)
            return NULL;
        BiTree T;
        T =  x[front];
        return T;
    }
}queues;

typedef struct Stack{ 
    // 自己构造栈
    BiTree *tt;
    int top;
    int size;
    void InitStack()
    {
        tt= ( BiTree *)malloc(n*sizeof(Tree));

        top=0;
        size=n;
    }
    bool emptys()
    {
        if(top==0)
            return true;
        return false;
    }
    void Push_back(BiTree num)
    {
        tt[top++]=num;
    }
    void Pop()
    {

        if(top==0)return;
        top--;
        //num=x[--top];
    }
    BiTree Gettop()
    {
        if(top==0) return NULL;
        return tt[top-1];// top
    }
}stacks;

1) 采用下列方法之一建立二叉树的二叉链表：

a) 输入完全二叉树的先序序列，用#代表虚结点（空指针），如ABD###CE##F##，建立二叉树的二叉链表。

code 
++
/**
 * 先序建立
 * @param T [description]
 */
void build_frist(BiTree &T)
{
    char ch;
    scanf("%c",&ch);
    if(ch=='#')
        T=NULL;
    else
    {
        T= new Tree ;
        T->x=ch;
        build_frist(T->lson);
        build_frist(T->rson);
    }
}

b) 已知二叉树的先序遍历序列和中序遍历序列。

code 
++
/**
 * [pre_mid_build 先序+中序建立二叉树]
 * @param Fi [先序]
 * @param In [中序]
 * @param l1 [先序左端下标]
 * @param h1 [先序右端下标]
 * @param l2 [中序左端下标]
 * @param h2 [中序右端下标]
 * 初始 l1 = l2 = 0 , h1 = h2 = n;
 */
BiTree pre_mid_build(BiTree Fi[],BiTree In[],int l1,int h1,int l2,int h2)
{
	BiTree T = new Tree;
	T->data = Fi[l1];
	for(int i = l2;In[i]!=Fi[l1] ; i++);
	int llen = i - l2;
	int rlen = h2 - i;
	if(llen)
		T->lchild = pre_mid_build(Fi,In,l1+1,l1+llen,l2,l2+llen-1);
	else
		T->lchild = NULL;
	if(rlen)
		T->rchild = pre_mid_build(Fi,In,h1-rlen+1,h1,h2-rlen+1,h2);
	else
		T->rchild = NULL;
	return T;
}

/**
 * 已知先序和中序 建立二叉树
 * @param T  [description]
 * @param Fi [description]
 * @param In [description]
 * @param n  [description]
 */
void build(BiTree &T,char *Fi,char *In,int n)
{
    if(n<1)
    {
        T=NULL;
        return;
    }
    int i=0,l1=0,l2=0,p=0,m=0;
    char lson[120],rson[120];
    char str1[120],str2[120];
    mem(lson,0);
    mem(rson,0);
    T= new Tree;
    T->x=Fi[0];
    while(In[i]!=Fi[0]) i++;
    l1=i; l2=n-i-1;
    int temp=i;
    for(int j=1;j<=temp;j++)
        lson[j-1]=Fi[j];
    for(int j=temp+1;j<n;j++)
    {
        rson[j-temp-1]=Fi[j];
        str2[j-temp-1]=In[j];
    }
    for(int j=0;j<temp;j++)
        str1[j]=In[j];
    if(!lson[0])
        T->lson=NULL;
    else
        build(T->lson,lson,str1,l1);
    if(!rson[0])
        T->rson=NULL;
    else
        build(T->rson,rson,str2,l2);
}

void frist_and_mid()
{
    cout<<"*****************************"<<endl;
    BiTree T2;
    char str1[120],str2[120],str3[120];
    printf("input of the first :\n");
    scanf("%s",str1);
    printf("input of the mid :\n");
    scanf("%s",str2);
    int len=strlen(str1);
    build(T2,str1,str2,len);
    printf("构造的二叉树 后序遍历为: \n");
    query(T2,3);
    cout<<"\n*****************************"<<endl;
}

c) 已知二叉树的中序遍历序列和后序遍历序列，建立二叉树的二叉链表。

++

2) 写出对用二叉链表存储的二叉树进行先序、中序和后序遍历的递归算法

code 
++
/**
 * 三种递归 1先序 2中序与 3后序
 * @param T    [description]
 * @param oper [description]
 */
void query(BiTree T,int oper)
{
    if(T)
    {
        if(oper==1)
            printf("%c ",T->x);
        query(T->lson,oper);
        if(oper==2)
            printf("%c ",T->x);
        query(T->rson,oper);
        if(oper==3)
            printf("%c ",T->x);
    }
}

3) 写出对用二叉链表存储的二叉树进行先序遍历的非递归算法。

code 
++
/**
 * 非递归先序
 * @param T [description]
 */
void query_frist(BiTree T)
{
    stacks S;
    S.InitStack();
    S.Push_back(T);

    while(!S.emptys())
    {
        while(S.Gettop()!=NULL)
        {
            printf("%c ",S.Gettop()->x);
            S.Push_back(S.Gettop()->lson);
        }
        S.Pop();
        if(!S.emptys())
        {
            BiTree Temp;
            Temp=S.Gettop();
            S.Pop();
            S.Push_back(Temp->rson);

        }
    }
}

4) 写出对用二叉链表存储的二叉树中序遍历的非递归算法。

code 
++
/**
 * 非递归中序
 * @param T [description]
 */
void query_mid(BiTree T) 
{
    stacks S;
    S.InitStack();
    S.Push_back(T);
    while(!S.emptys())
    {
        while(S.Gettop()!=NULL)
        {
            S.Push_back(S.Gettop()->lson);
        }
        S.Pop();
        if(!S.emptys())
        {
            BiTree Temp;
            Temp=S.Gettop();
            printf("%c ",Temp->x);
            S.Pop();
            S.Push_back(Temp->rson);
        }
    }
}

5) 写出对用二叉链表存储的二叉树后序遍历的非递归算法。

code 
++
/**
 * 非递归后序
 * @param T [description]
 */
void query_last(BiTree T)
{
    stacks S;
    S.InitStack();
    S.Push_back(T);
    while(!S.emptys())
    {
        while(S.Gettop()!=NULL)
        {
            S.Push_back(S.Gettop()->lson);
        }
        S.Pop();
        if(!S.emptys())
        {
            if(S.Gettop()->rson)
                S.Push_back(S.Gettop()->rson);
            else
            {
                BiTree  Temp;
                Temp=S.Gettop();
                printf("%c ",Temp->x);
                S.Pop();
                while(S.Gettop()!=NULL&&!S.emptys()&&S.Gettop()->rson==Temp)
                {
                    printf("%c ",S.Gettop()->x);
                    Temp=S.Gettop();
                    S.Pop();
                }
                if(!S.emptys())
                {
                    S.Push_back(S.Gettop()->rson);
                }

            }
        }
    }
}

/**
 * [PostOrder 后序遍历二叉树非递归]
 * @param T [Bitree]
 */
void PostOrder(BiTree T)
{
	InitStack(S);
	BiTree p = T;
	BiTree r = NULL;
	while(p || !IsEmpty(S)){
		if(p) // 走到最左边
		{ 
			Push(S,p);
			p = p->lchild;
		}
		else
		{
			GetTop(S,p); 
			if(p->rchild && p->rchild != r) // 右子树存在且未被访问
			{
				p = p->rchild; // 转向右
				Push(S,p);// 入栈
				p = p->lchild; // 转向左
			}else{
				Pop(S,p);
				visit(p->data);
				r= p ;
				p = NULL;
			}
		}
	}
}

6) 写出对用二叉链表存储的二叉树进行层次遍历算法。

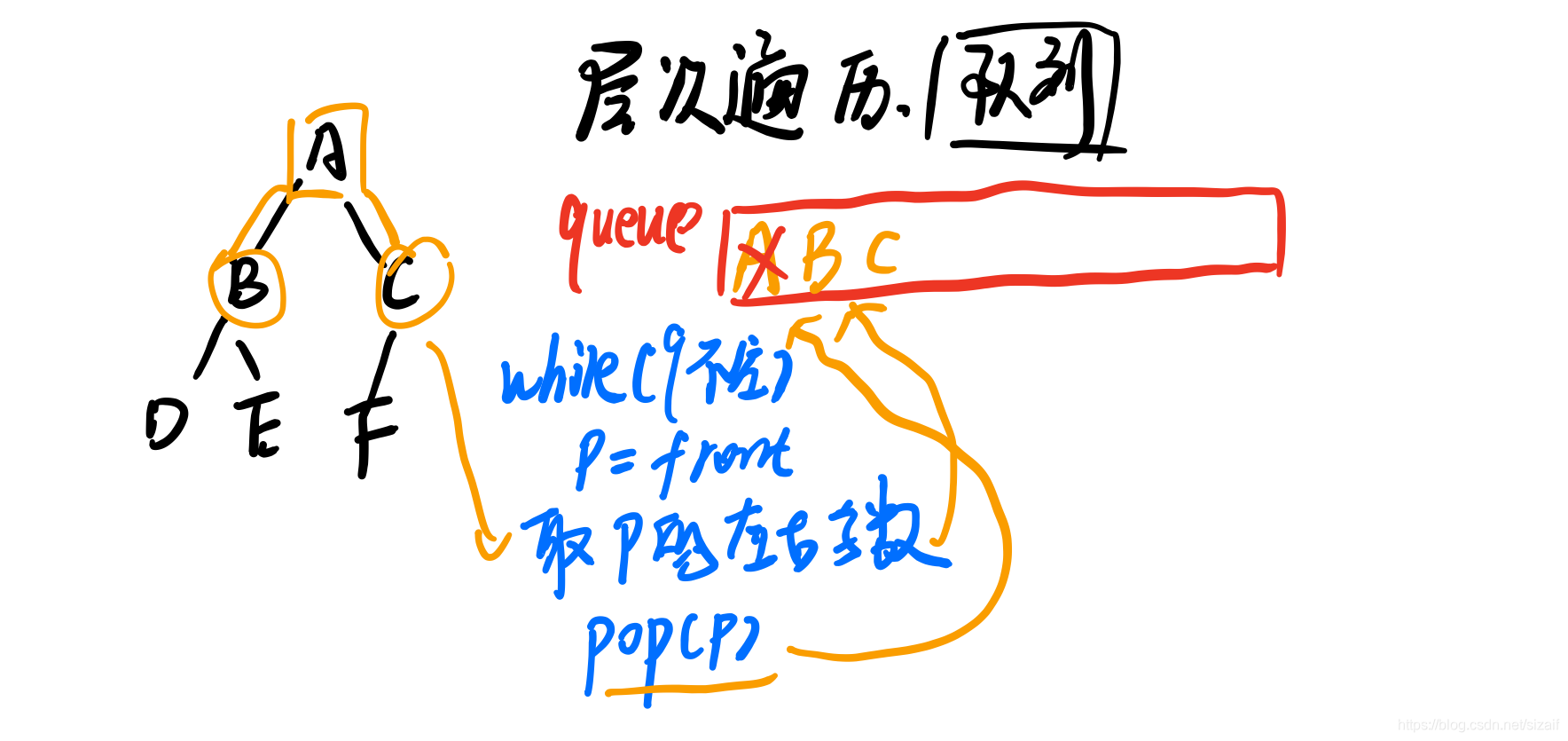
在这里插入图片描述

code 
++
/**
 * [Invertlevel 层次遍历,自下而上,自左到右]
 * @param T [BiTree]
 * 二叉树自下而上,自左到右
 * 正常层次遍历, 出队时入栈
 * 最后依次出栈为结果
 */
void Invertlevel(BiTree T)
{
	Stack<int> S;
	Queue<int> Q;
	BiTree p;
	if(T)
	{
		InitQueue(Q);
		InitStack(S);	
		EnQueue(Q,T);
		while(!IsEmpty(Q)) 
		{
			DeQueue(Q,p);
			Push(S,p); //  出队,入栈
			if(p->lchild)
				EnQueue(Q,p->lchild);
			if(p->rchild)
				EnQueue(Q,p->rchild);   
		}
		while(!IsEmpty(S)) {
		    Pop(S,p);
		    visit(p->data); // 自下而上,自左到右
		}
	}
}

7) 递归实现求二叉树的所有叶子数。

在这里插入图片描述

code 
++
/**
 * 求二叉树的所有叶子数]
 * @param T [description]
 */
void query_leaf(BiTree T){
	if(!T)
		return 0;
	if(T->lson == NULL && T->rson == NULL)
		return 1;
	return query_leaf(T->lson)+query_leaf(T->rson);
}

8) 递归实现求二叉树的所有结点总数。

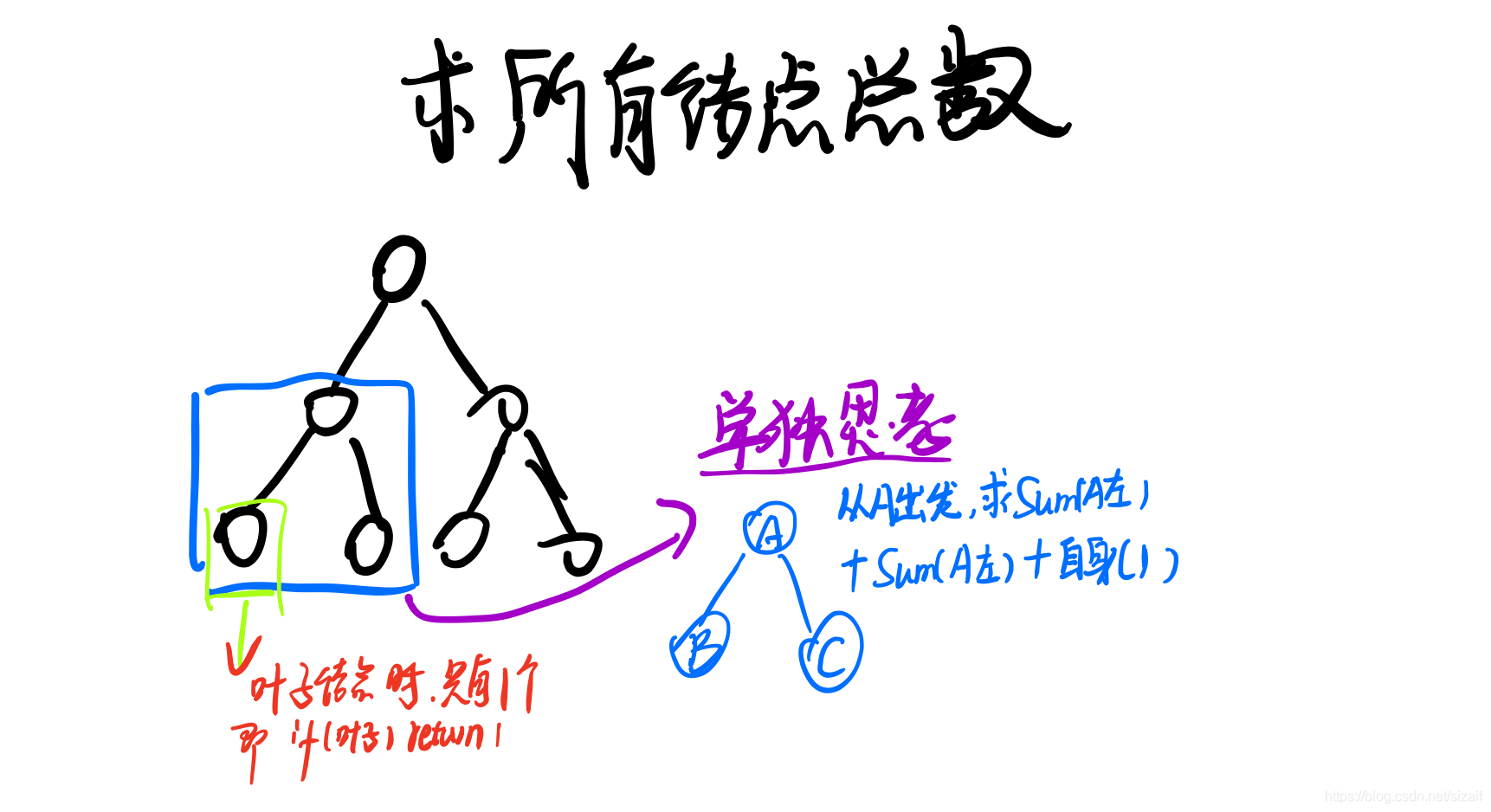
在这里插入图片描述

++
int query_node(BiTree T)// 节点总个数 
{
    if(!T)
        return NULL;
    if(T->lson == NULL && T->rson == NULL)
        return 1;
    return query_node(T->lson) + query_node(T->rson) + 1;
}

8+) 求二叉树第k层的结点个数

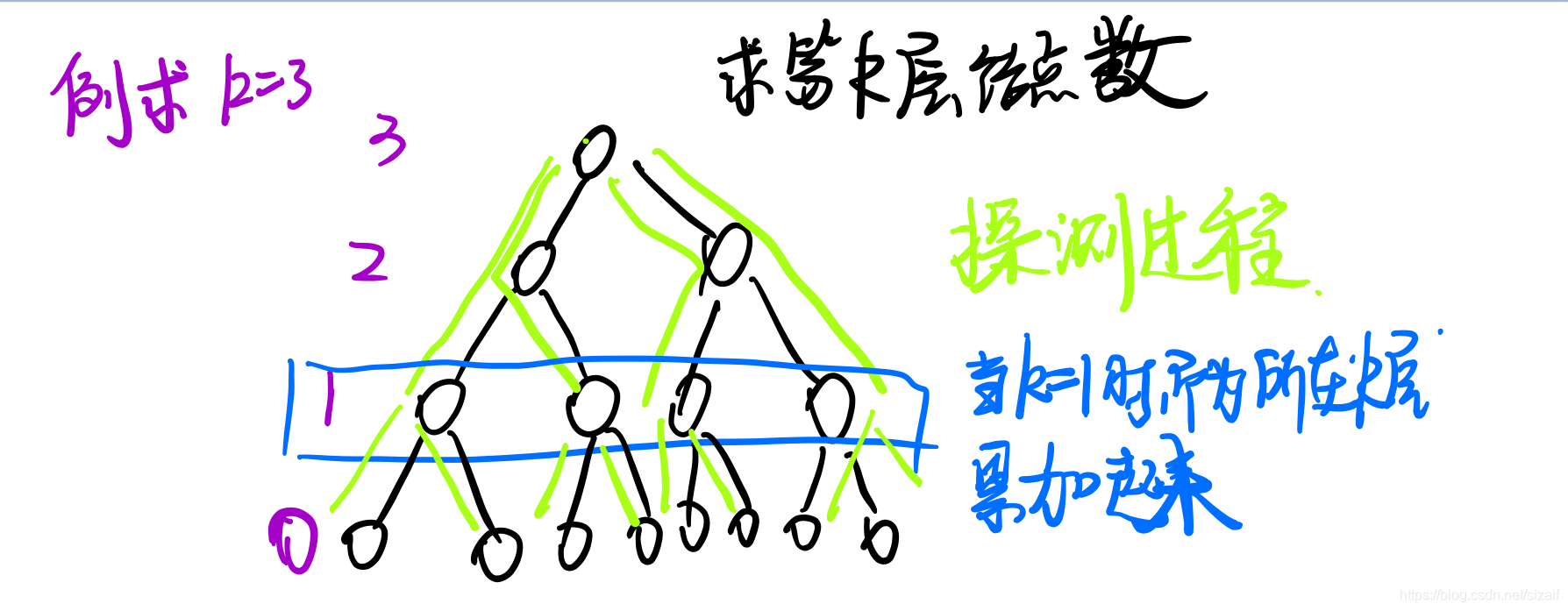
在这里插入图片描述

code 
++
/**
 * 求二叉树第 k 层的结点个数
 * 思想: 如图
 * @param  T [description]
 * @param  k [第k层]
 * @return   [description]
 */
int query_levelk(BiTree T,k){
    if(!T) return 0;
    if(k <= 0) return 0;
    if(k <= 1) return 1;
    return query_levelk(T->lson,k-1) + query_levelk(T->rsom,k-1);
}

9) 判断完全二叉树

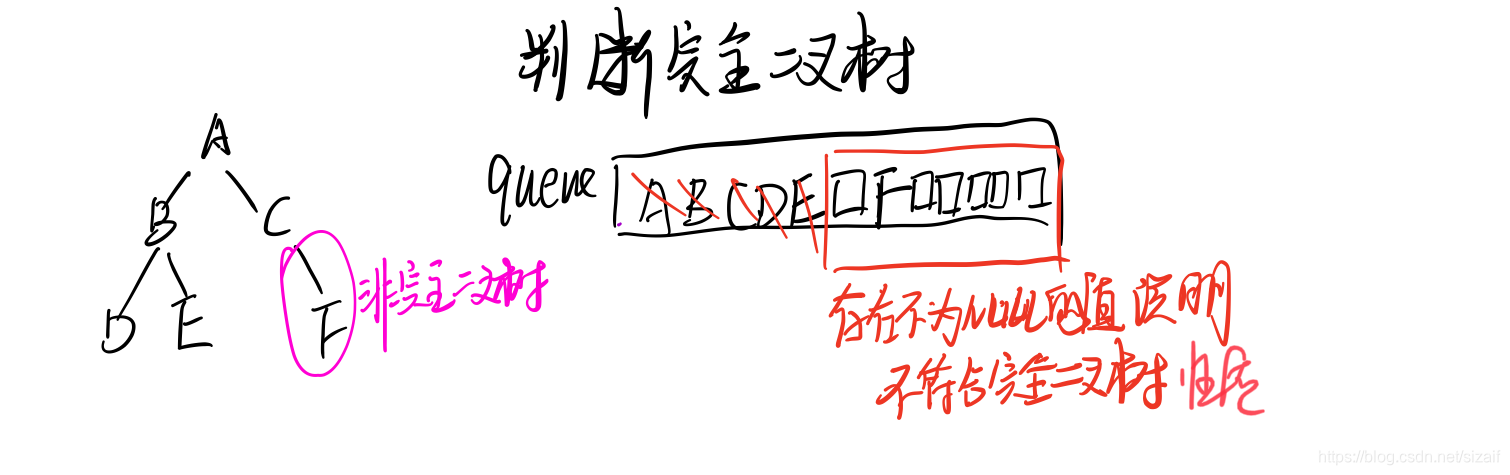
在这里插入图片描述

code 
++
/**
 * 判断完全二叉树 
 * @param  T [description]
 * @return   [description]
 */
bool judge(Bitree &T)
{
    //1 2 4 8 -1 -1 9 -1 -1 5 10 -1 -1 -1 3 6 -1 -1 7 -1 -1
    queue<Bitree>Q;
    Bitree pre;
    Q.push(T);

    while(Q.front() != NULL)
    {
        pre = Q.front();
        Q.pop();
        Q.push(pre->lson);
        Q.push(pre->rson);
    }
    while(!Q.empty())
    {
        pre = Q.front();
        Q.pop();

        if(NULL != pre)
            return false;
    }
    return true;

}

10) 递归实现求 二叉树高度(深度)

在这里插入图片描述

code 
++
/**
 * 二叉树高度 
 * @param  T [description]
 * @return   [description]
 */
int deep_tree(Bitree &T)
{
    if(!T)
        return 0;
    int left = deep_tree(T->lson);
    int rig = deep_tree(T->rson);
    return left > rig  ? (left+1):(rig+1);
}

11) 非递归求二叉树高度(深度)(利用层次遍历)

在这里插入图片描述

code 
++
/**
 * [BtDepth 非递归求二叉树高度]
 * @param T [BiTree]
 *  数组模拟队列,level 记录层数,
 *  每次层次遍历出队列时,与last指针比较,若两者相同,则层数+1;
 */
void BtDepth(BiTree T)
{
	if(!T)
		return 0;
	int front = -1 , rear = -1;
	int last = 0 , level = 0;
	BiTree Q[MAXN];
	Q[++rear] = T;
	BiTree p;
	while(front <= rear) {
	    p = Q[++front];
	    if(p->lchild)
	    	Q[++rear] = p->lchild;
	    if(p->rchild)
	    	Q[++rear] = p->rchild;
	    if(front == last){ // 该层最右结点
	    	level++;
	    	last = rear;  //  更新
	    }
	}
}

11+) 孩子兄弟表示法求树的深度

code 
++
/**
 * [Height_CS 孩子兄弟表示法求树的深度]
 * @param  T [description]
 * @return   [description]
 */
int Height_CS(CSTree T)
{
	int hc,hs;
	if(T == NULL)
		return 0;
	else
	{
		hc = Height_CS(T->fichild); // 第一子树高
		hs = Height_CS(T->nextchild); // 兄弟树高
		return hc+1 > hs ? hc+1 : hs;
	}
}

12) 判断平衡二叉数是否平衡

code 
++
/**
 * [judge_AVL 判断二叉排序树,是否平衡]
 * @param T       [description]
 * @param balance [description]
 * @param h       [description]
 * balanc = 1 平衡, 0 不平衡
 *  空树 , 仅有根节点,  平衡
 */
void judge_AVL(BiTree T,int &balance ,int &h)
{
	int bl = 0, br = 0, hl = 0 , hr = 0;
	if(T == NULL) // 空树 ,高度为 0 
	{
		h = 0; balance = 1;
	}
	else if(T->lchild == NULL &&  T->rchild == NULL) // 仅有根节点,  高度为1 
	{
		h = 1, balance = 1 ;
	}
	else
	{
		judge_AVL(T->lchild,bl,h1); 
		judge_AVL(T->rchild,br,h2);
		h = (hl> hr ? hl:hr) +1; 
		if(abs(hl-hr) < 2) // 高度差 小于2 
			balance = bl && br;  //逻辑与  当左右都平衡时, 平衡
		else
			balance = 0;
	}
}

13) 递归实现求二叉树双分支节点树

code 
/**
 * [DsonNode 递归实现求二叉树双分支节点树]
 * @param  T [二叉链表]
 * @return   [节点数]
 */
int DsonNode(BiTree T)
{
	if(T==NULL)
		return 0;
	else if(T->lchild !=NULL && T->rchild !=NULL ) // 左右孩子都有
			return DsonNode(T->lchild) + DsonNode(T->rchild) +1;
	else
			return DsonNode(T->lchild) + DsonNode(T->rchild);
}

14) 递归实现左右孩子互换

code 
++
/**
 * [Swap_child 递归实现左右孩子互换]
 * @param T [description]
 * 先换T结点 左子树左右孩子
 * 再换右子树, 
 * 最后节点的孩子互换
 */
void Swap_child(Bitree T)
{
	if(T)
	{
		Swap_child(T->lchild); // 先左子树
		Swap_child(T->rchild); // 右子树
		Bitree temp = T->lchild; // 左右孩子互换
		T->lchild = T->rchild;
		T->lchild = temp;
	}
}

15) 删除二叉树中每个元素值 为x的结点

code 
++
/**
 * [Search 删除二叉树中每个元素值 为x的结点]
 * 并删去以他为根的子树
 * @param T [description]
 * @param x [description]
 * 后序遍历二叉树, 层次遍历找到结点的父节点
 */
void Search(BiTree T,ElemType x){
	BiTree Q[];
	if(T)
	{
		if(T->data == x)
		{
			DeleteXTree(T);
			exit(0);
		}
		InitQueue Q;
		EnQueue(Q,T);
		while(!IsEmpty(Q))
		{
			DeQueue(Q,p);
			if(p->lchild){ // 左非空
				if(p->lchild->data == x)  // 左子树符合, 删除左子树
				{
					DeleteXTree(p->lchild);
					p->lchild =  NULL;
				}
				else  // 父节点左子树置为空
					EnQueue(Q,p->lchild);  //左子女入队列
			}
			if(p->rchild)  // 右子树符合, 删除右子树
			{
				if(p->rchild->data == x)
				{
					DeleteXTree(p->rchild);
					p->rchild = NULL;
				}
				else
					EnQueue(Q,p->rchild); // 右子女入队列
			}
		}
	}
}

16) 求先序遍历中第k个结点的值

code 
++
/**
 * [PreNode 求先序遍历中第k个结点的值]
 * @param  Bt [description]
 * @param  k  [description]
 * @return    [description]
 */
int count = 1;
ElemType PreNode(BiTree T, int k)
{
	if(T == NULL)
		return '#';
	if( count == k)
		return T->data;
	count++;
	ch = PreNode(T->lchild,k); // 左子树返回该值
	if(ch != '#')
		return ch;
	ch = PreNode(T->rchild,k); // 右子树递归查找
		return ch;
}

17) 求代权路径长度和

code 
++
/**
 * [Wpl_preOreder 求代权路径长度和]
 * @param  T    [description]
 * @param  deep [description]
 * @return      [description]
 * 2014 408 真题 , 王道127页
 */
int Wpl(BiTree T)
{
	return Wpl_preOreder(T,0);
}
int wpl = 0;
int Wpl_preOreder(BiTree T,int deep)
{
	if(T->lchild == NULL && T->rchild == NULL) // 叶节点 返回 wp
		wpl += deep * T->data;
	if(T->lchild != NULL)
		Wpl_preOreder(T->lchild,deep+1);
	if(T->rchild != NULL)
		Wpl_preOreder(T->rchild,deep+1);
	return wpl;
}

18) 求非空二叉树的宽度

code 
++
/**
 * [BTWidth 求非空二叉树的宽度]
 * @param  T [description]
 * @return   [description]
 * 层次遍历求所有点的层次,将所有节点和对应层次放在一个队列中
 * 扫描队列,求最大层次节点总数
 */
typedef struct{
	BiTree data[MAXN];// 存放指针
	int level[MAXN];//层次
	int front,rear;
}Que;
int BTWidth(BiTree T)
{
	BiTree p;
	Que.front = Que.rear = -1;
	Que.rear ++;
	Que.data[Que.rear] = T; // 入队
	Que.level[Que.rear] = 1;// 层次为1;
	int k,Max,n;
	while(Que.front < Que.rear)
	{
		Que.front ++; // 出队
		p = Que.data[Que.front];
		k = Que.level[Que.front];
		if(p->lchlid != NULL) // 左孩子进队列
		{
			Que.rear++;
			Que.data[rear] = p->lchlid;
			Que.level[rear] =  k + 1;
		}
		if(p->rchild!=NULL) // 右孩子进队列
		{
			Que.rear++;
			Que.data[rear] = p->rchlid;
			Que.level[rear] =  k + 1;	
		}
	}
	Max = -1, k = 1;
	int i = 0;
	while( i < Que.rear) {
	    n = 0;
	    while(i<Que.rear && Que.level[i] == k) {  // 统计第k曾节点数
	        n++;
	        i++;
	    }
	    k = Que.level[i];
	    if( n > Max)
	    	Max = n;
	}
	return Max;
}

19) 判断两颗二叉树是否结构相同

在这里插入图片描述

code 
++
/**
 * [判断两个二叉树结构是否相等]
 * @param  T1 [description]
 * @param  T2 [description]
 * @return    [description]
 */
int isEqual(BiTree T1,BiTree T2){
	if( !T1 && !T2) return 1;
	if( !T1 || !T2) return 0;
	return isEqual( T1->lson,T2->lson) && isEqual(T1->rson,T2->rson); 
}

20) 求两个结点的最低(近)公共祖先结点

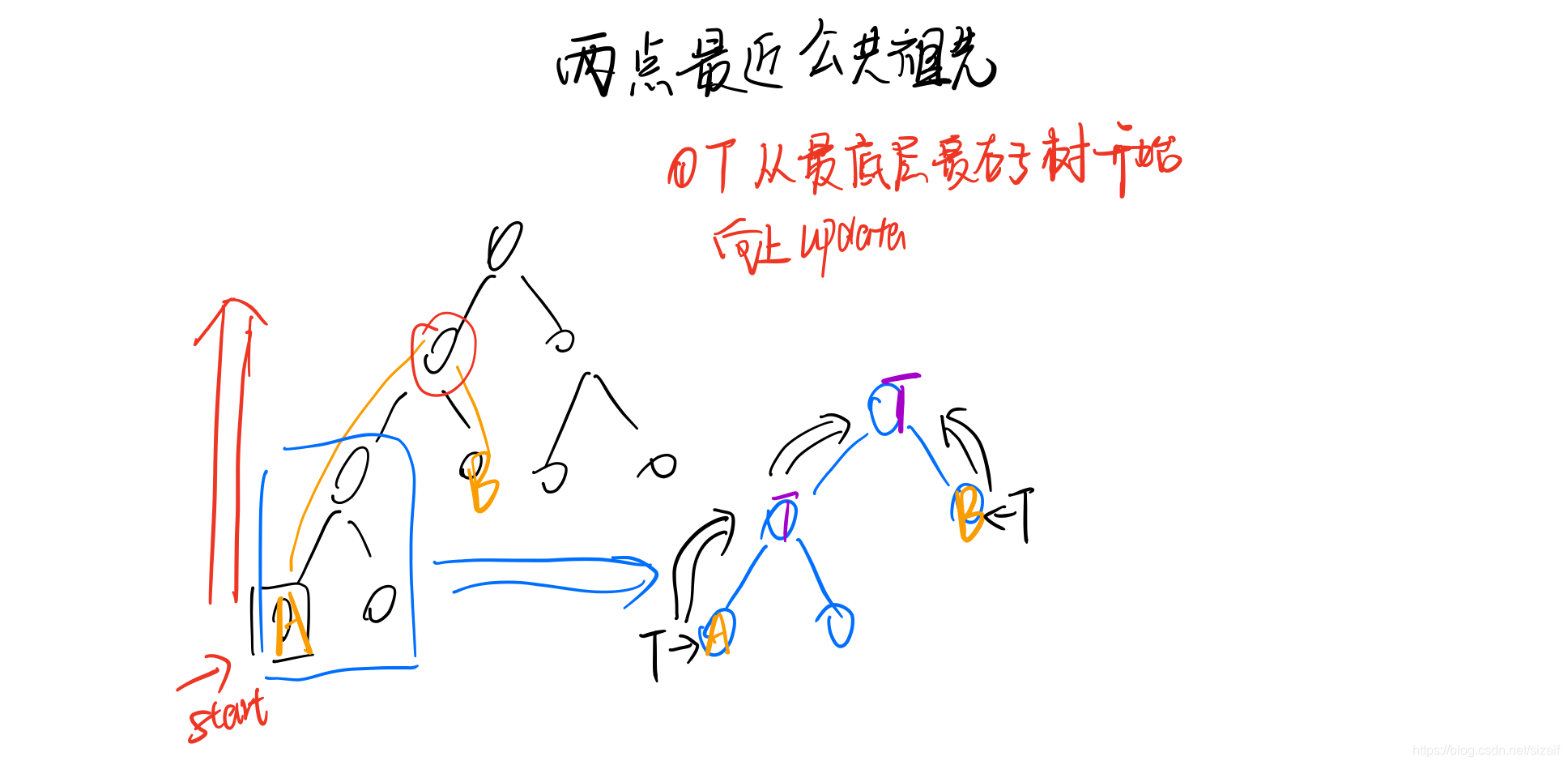
在这里插入图片描述

code 
++
/**
 * [求两个结点的最低公共祖先结点]
 * @param  T [description]
 * @param  A [description]
 * @param  B [description]
 * @return   [description]
 */
BiTree lowAnc(BiTree T,BiTree A,BiTree B){
	if( !T) return NULL;
	if( T == A || T == B) return T; // 说明在某左子树或右子树中找到目标结点

	BiTree left = lowAnc(T->lson,A,B);
	BiTree right = lowAnc(T->rson,A,B);
    
	// 当在左子树和右子树中都找到A,B 说明是最近的公共祖先
	if( left != NULL && right != NULL) 
		return T;
    //对一个底层向上更新的根结点来说，只在左子树或右子树找到了目标结点，则返回找到的结点。
	return !left ? right:left; 
}

20+) 求任意两结点距离

在这里插入图片描述

code 
++
/**
 * [求两个结点的最低公共祖先结点]
 * @param  T [description]
 * @param  A [description]
 * @param  B [description]
 * @return   [description]
 */
BiTree lowAnc(BiTree T,BiTree A,BiTree B){
	if( !T) return NULL;
	if( T == A || T == B) return T; // 说明在某左子树或右子树中找到目标结点

	BiTree left = lowAnc(T->lson,A,B);
	BiTree right = lowAnc(T->rson,A,B);

	if( left != NULL && right != NULL) // 当在左子树和右子树中都找到A,B 说明是最近的公共祖先
		return T;
	return !left ? right:left; //对一个底层向上更新的根结点来说，只在左子树或右子树找到了目标结点，则返回找到的结点。
}
/**
 * [求最近公共祖先到目标p的距离]
 * @param  T [description]
 * @param  p [description]
 * @return   [description]
 */
int CalDistance(BiTree T,BiTree p){
	if( !T ) return -1;
	if( T == p) return 0;
	// 先在左子树找
	int res = CalDistance(T->lson,p);
	// 如果未找到,在右子树中找
	if( res == -1)
		res = CalDistance(T->rson,p);
	// 找到, 距离+1 
	if( res != -1)
		return res + 1; // 如果带权值, 这里改成+权值
	return -1;
}
/**
 * [求树中A-B的距离]
 * @param  T [description]
 * @param  A [description]
 * @param  B [description]
 * @return   [description]
 */
int Dis_A_B(BiTree T,BiTree A,BiTree B){

	//找到最低公共祖先结点
	BiTree lowanc = lowAnc(T,A,B);
	// 求最近最近公共祖先结点到两目标结点的距离之和
	return  CalDistance(lowanc,A) + CalDistance(lowanc,B);
}

20++) 找出二叉树中某个结点的所有祖先结点

在这里插入图片描述

code 
++
/**
 * 找出二叉树中某个结点的所有祖先结点
 * @param  T [description]
 * @param  A [description]
 * @return   [description]
 */
int FindAllAnc(BiTree T, BiTree A){
	
	// 未找到
	if( !T ) return 0;
	//  找到目标结点
	if(　T == A) return 1;
	// 如果在左子树或右子树中找到输出此祖先结点
	if( FindAllAnc(T->lson,A) || FindAllAnc(T->rson,A) )
	{
		// 或者其他操作
		cout<<T->data<<endl;
		return 1;
	}
	return 0;
}

博客内容遵循 署名-非商业性使用-相同方式共享 4.0 国际 (CC BY-NC-SA 4.0) 协议

本文永久链接是：https://www.sizaif.com/posts/cfa0d73d/

更新于：2021年9月19日

C++

算法

次浏览

评论吧



本站总访问量为 次 访客数为 人

鲁 ICP 备 20018157 号-1
Copyright 2021 - 2022 sizaif. All Rights Reserved
腾
龍
跃
虎