方法一: mod移位思想

													图一：

/**
 * 思路: 
 * 运用mod的思想, 将n复制成2n的数组 如图一所示; 那么循环有移 逃不出2n内
 * 右移后的结果为： (i+k)   缩到n内的话 就是 (i+k)%n
 * 实际上只需要用另外一个数组B[] 来存取 原数组A[] 的内容 即 B[i] = A[(i+n-k)%n];
 * 但是 这样的话  空间复杂度就为 O(n), 时间复杂度为 O(n);
 */
	for(int i = 0; i< n ;i++)
	{
		b[ i ] = a[ (i + n - k)%n];
	}

方法一plus：

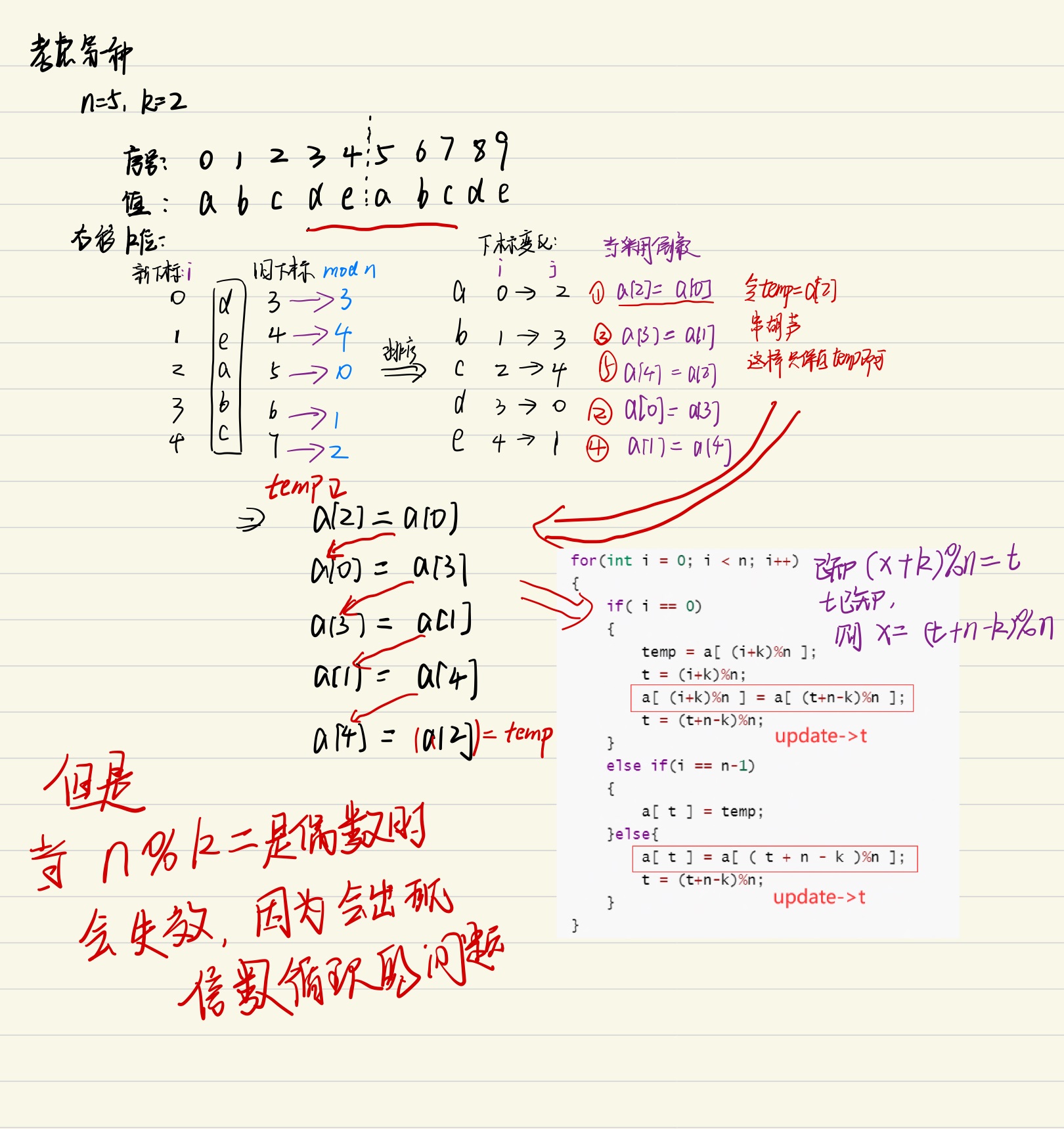
会出现如下的情况：

改进-最大公约数GCD

/**
* 将方法加以改进 
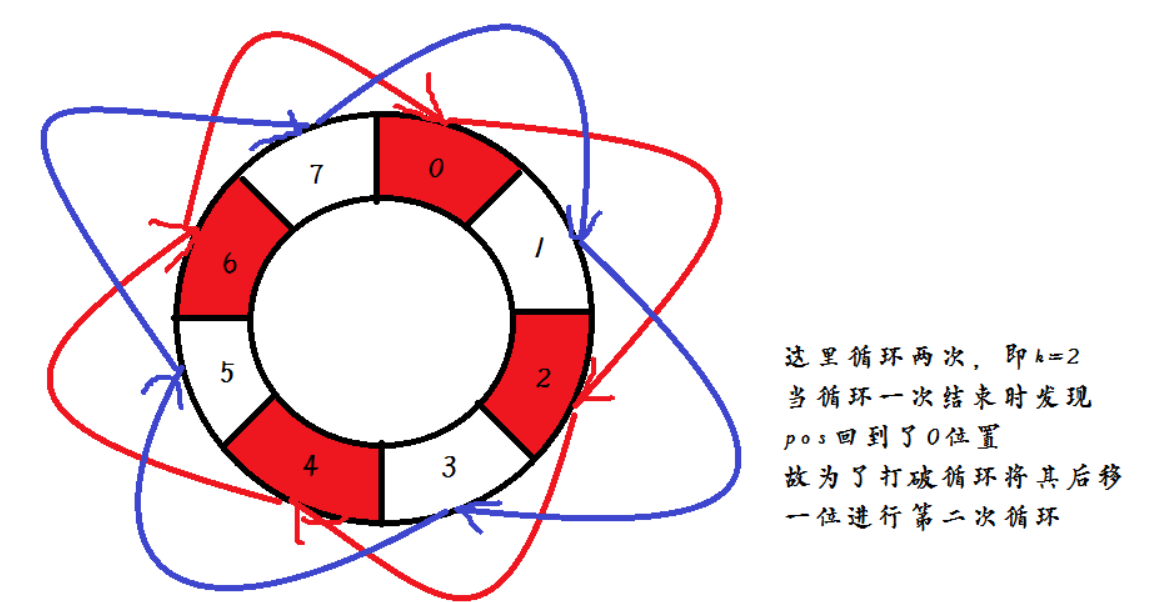
* 将其按照 k 步进行分组，   类似于希尔排序的思想， 每间隔k的位置构成一组，那么我们
* 的所谓右移只是在这每一组中组内移动，类似下图
* 那么我们只需要确定我们要循环几次就可以找到答案呢？
* 答案是确定的只需要找到他们的 gcd ，
* 然后记录下开始位置，采用 反求x的方法 即  （x+k)%n = t, t,n,k已知 求未知数x
*  x = (t+n-k)%n; 当 x == 开始位置时停止,进入下一组
*  时间复杂度O(n) , 空间复杂度O(1)
*/
int Gcd(int a,int b){ 
	return b==0?a:Gcd(b,a%b); // 辗转相除法求GCD
}
void fun(int a[],int n,int k){
    
    int gcd = Gcd(n,k);
	int t,temp,j;
	for(int i = 0 ;i < gcd; i++)
	{
		temp = a[i]; // 记录开始位置 
		t = i;
		while(1){
			
			j = ( t + n - k )%n;
			if( j == i)	 break; // 循环到自己跳出 
			a[t] = a[j];
			t = j;
		}
		a[t] = temp;
	}
}

==验证：==

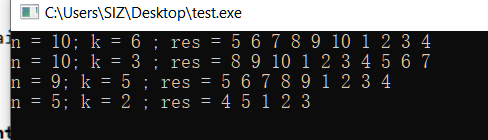
方法二：倒叙移位

/** ``````````````````````分割线``````````````````````````````


* 将空间复杂度降到O(1)
* 所以考虑只用一个辅助结点的优化方法
* 
* 第一种 循环k次， 从后面开始移动，  空间复杂度为O(1) ,但时间复杂度为 O(kn)
*
*/
for(int i = 0; i < k; i++){
       int temp = a[n - 1];
       for(int j = n-1; j > 0; j --){
           a[j] = a[j-1];
       }
           a[0] = temp;
   }

方法三：递归调用

/** ``````````````````````分割线``````````````````````````````
* 将空间复杂度降到O(1)
* 所以考虑只用一个辅助结点的优化方法
* 
* 第二种 采用递归反转的方式  空间复杂度为O(1) ,时间复杂度为 O(n)
* 先递归反转前 （n-k)位  在反转后 k位  最后 全部反转
*/

   void reverse(int a[],int l,int r){
       for(; l < r; l++,r--)
       {
           int temp = a[l];
           a[l] = a[r];
           a[r] = temp;
       }
   }
int main(){
       
       reverse(a,0,n-k-1);
    reverse(a,n-k,n-1);
    reverse(a,0,n-1); 
       
       return 0;
   }